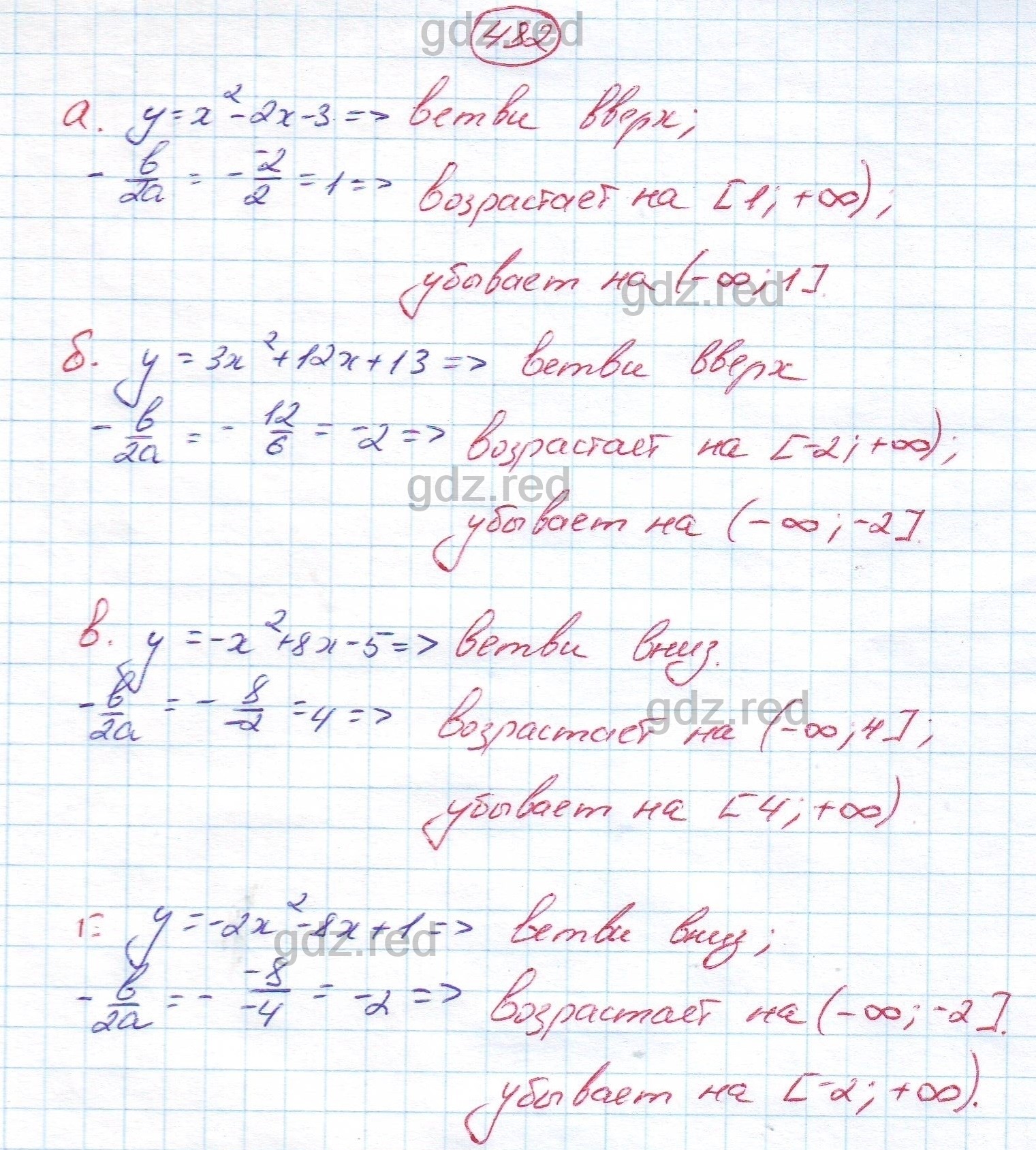Номер 482 — ГДЗ по Алгебре для 8 класса Учебник Никольский, Потапов, Решетников, Шевкин

Рассмотрим ответы на Номер 482 из учебника по алгебре для 8 класса Никольского
482. Доказываем. Докажите, что функция: а) у = х2 — 2х — 3 возрастает на промежутке [1; + ∞) и убывает на промежутке (-∞; 1]; б) у = Зх2 + 12x + 13 возрастает на промежутке [-2; + ∞) и убывает на промежутке (-∞; —2]; в) у = -x2 + 8x — 5 убывает на промежутке [4; + ∞) и возрастает на промежутке (-∞; 4]; г) у = -2×2 – 8x + 1 убывает на промежутке [-2; + ∞) и возрастает на промежутке (-∞; -2].