Решение №1
Решение №2
На этой странице рассмотрим все ответы на Номер 398 из учебника по математике 5 класс Дорофеев
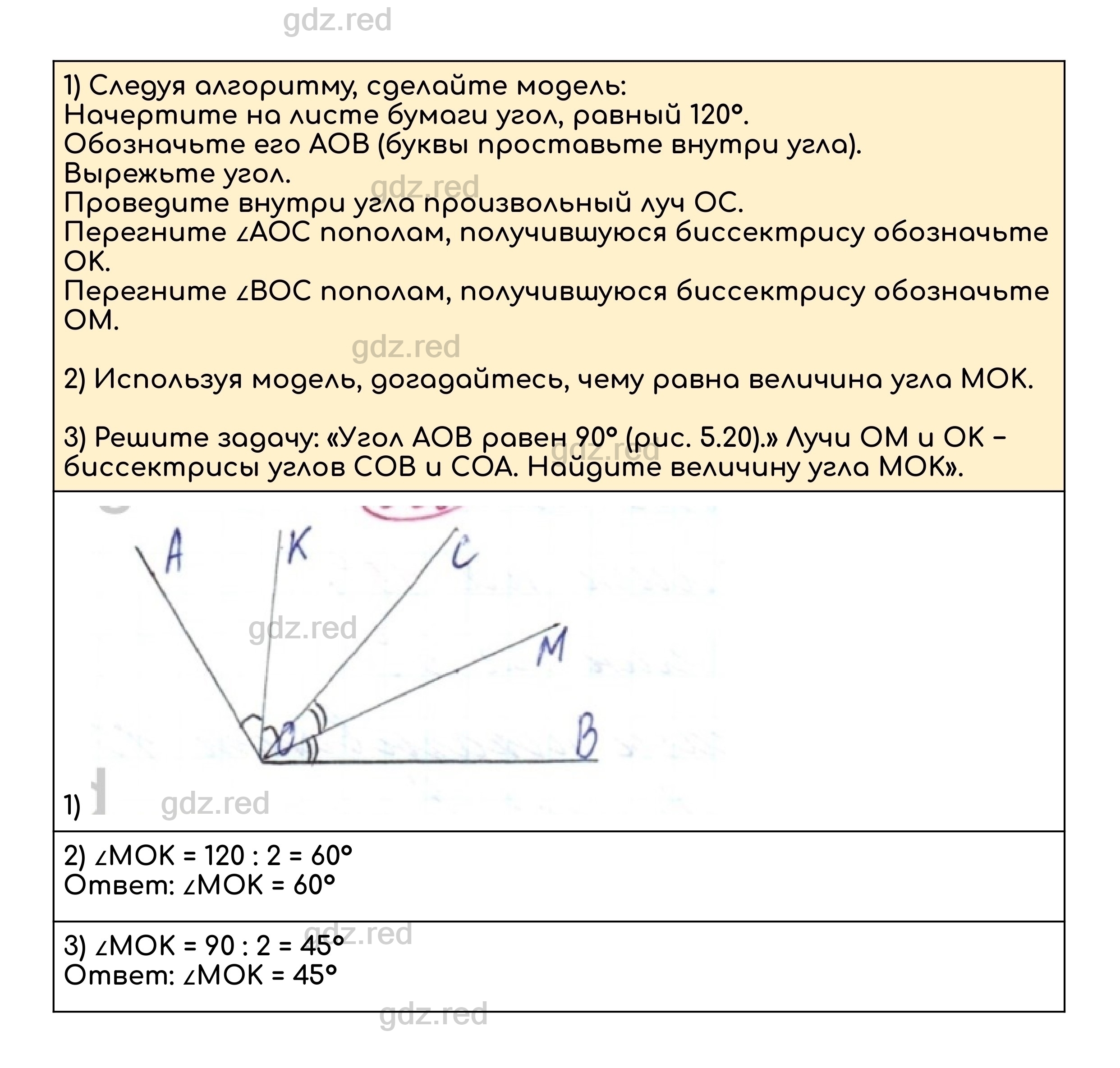
1) Следуя алгоритму, сделайте модель:
Начертите на листе бумаги угол, равный 120°.
Обозначьте его AOB (буквы проставьте внутри угла).
Вырежьте угол.
Проведите внутри угла произвольный луч OC.
Перегните ∠AOC пополам, получившуюся биссектрису обозначьте OK.
Перегните ∠BOC пополам, получившуюся биссектрису обозначьте OM.
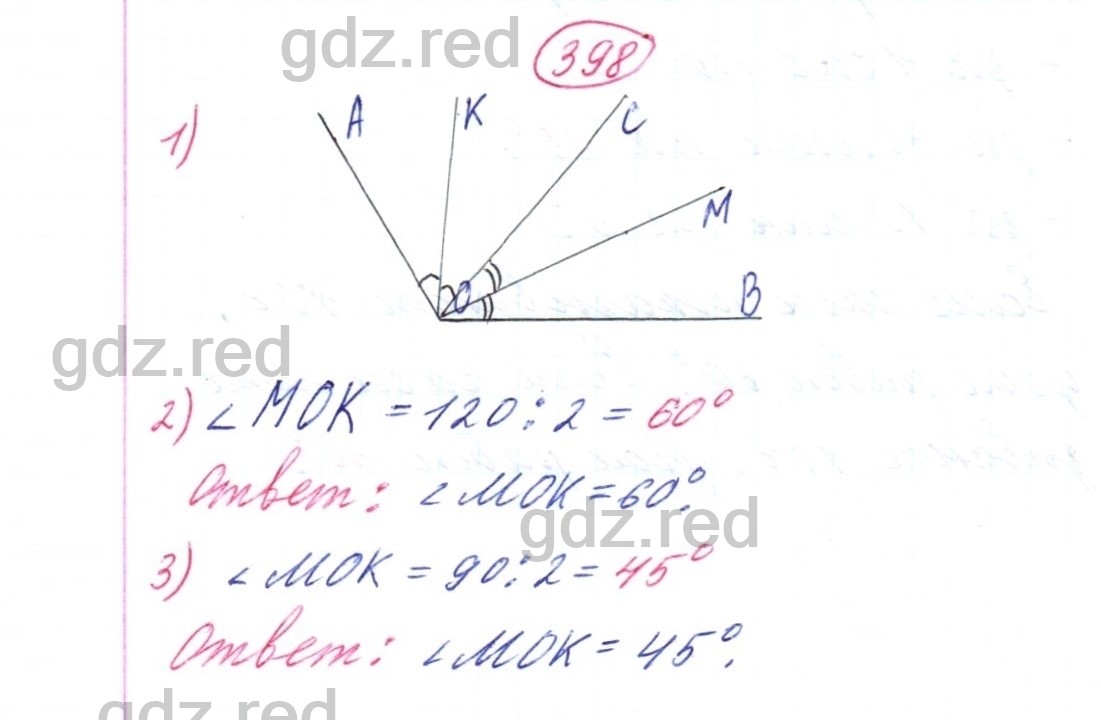
2) Используя модель, догадайтесь, чему равна величина угла MOK.
3) Решите задачу: «Угол AOB равен 90° (рис. 5.20).» Лучи OM и OK − биссектрисы углов COB и COA. Найдите величину угла MOK».
1) Следуя алгоритму, сделайте модель:
Начертите на листе бумаги угол, равный 120°.
Обозначьте его AOB (буквы проставьте внутри угла).
Вырежьте угол.
Проведите внутри угла произвольный луч OC.
Перегните ∠AOC пополам, получившуюся биссектрису обозначьте OK.
Перегните ∠BOC пополам, получившуюся биссектрису обозначьте OM.
2) Используя модель, догадайтесь, чему равна величина угла MOK.
3) Решите задачу: «Угол AOB равен 90° (рис. 5.20).» Лучи OM и OK − биссектрисы углов COB и COA. Найдите величину угла MOK».
Номера упражнений
«Чему Вы научились»